Pianos are strange beasts. Unlike guitars or violins where there is an established standard for how each string should be tuned, pianos are all tuned differently. This means that if you were to compare two freshly tuned pianos the notes would not match, even though each piano sounds in tune with itself. This article seek to explore why pianos are all tuned differently, how their tuning differs from one another, and why this is critical to getting the best sound out of each instrument.
If you have ever taken a basic physics class, you probably learned that a vibrating string produces something called harmonics. You may have also learned that harmonics are whole number multiples of the fundamental, which is the lowest sounding frequency. It turns out that this is not exactly true but we will get to that later. Let’s take a moment to review what harmonics are.
When a string is plucked, it vibrates back and forth at a specific rate determined by its length, mass, and tension. Change any one of these factors and the string will cause the string to vibrate at a different frequency. The frequency of vibration determines the pitch, which is the perceived height of the note. C-sharp for example produces a higher pitch than the note C because the length, mass, and tension of the string is different. Increasing the length or mass (weight) of a string lowers the pitch, while increasing the tension raises it. This is apparent if you simply look at a piano and notice that the low strings are very long and thick, while the high strings are very short and thin.
frequency = tension / (mass * length)
Strings do not only produce one vibration however. This main vibration is called the fundamental, but there are other lesser vibrations present in the string called harmonics. Suppose a string was tuned to vibrate at 100hz, meaning 100 times per second. According to what we learn in physics class it would also produce weaker vibrations at 200, 300, 400 hz, etc. However, what most of us learn in physics class is unfortunately wrong.
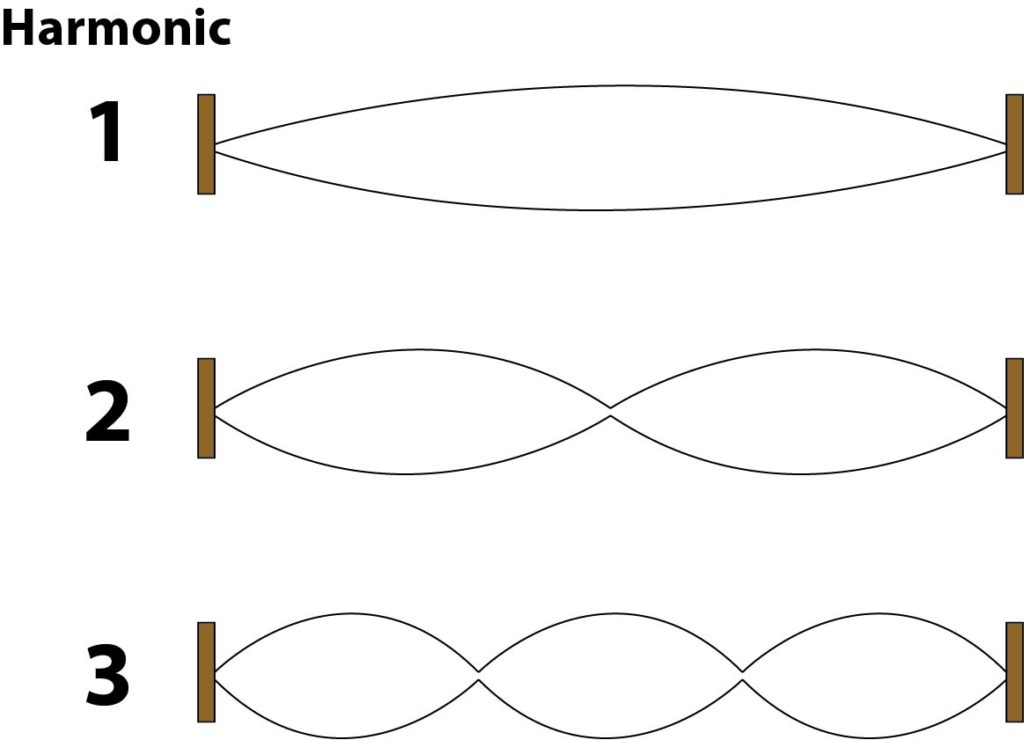
Vibrating strings possess something called inharmonicity. Inharmonicity is a measurement of how far off the harmonics are from their predicted values. As mentioned above, we would expect a string vibrating at 100hz to have harmonics at 200, 300, 400hz and so on. If a string were perfectly elastic, it would indeed produce perfect harmonics. However, due to the stiffness of the string, higher harmonic vibrations travel faster than lower ones meaning as you go up the harmonic series, the values deviate more and more from their predicted values. In other words, the higher you go in the harmonic series, the sharper the notes get. Here is a table showing actual inharmonicity values for middle C:
| Partial | Offset | Amplitude |
| 1 | 0 | 100 |
| 2 | 1.46 | 21 |
| 3 | 3.58 | 8 |
| 4 | 4.85 | 9.5 |
| 5 | 6.79 | 3.8 |
| 6 |
| 1.2 |
| 7 | 13.16 | 4.3 |
| 8 | 16.91 | 1.2 |
As harmonics are in no uncertain terms the ingredients that make up a note, getting a piano in tune means getting the harmonics to be in tune. Therefore, the first step in tuning a piano is to measure the inharmonicity, then calculate the ideal tuning that will yield the greatest alignment between the harmonics. As every make and model of piano differs in terms of the length, thickness and tension of the strings, that means every piano has a slightly different inharmonicity profile. The one exception would be that if you are tuning two pianos with the same make and model, such two Yamaha C5’s, you can then use the same inharmonicity profile.
When you are considering buying a larger vs. a smaller piano, you might be thinking that the only benefit of a larger piano is that it is louder. Actually this is not true. Larger pianos produce purer harmonics, and therefore sound more in tune than smaller pianos. Why? As we mentioned before if a string was perfectly elastic it could produce pure harmonics. Although no string can every be perfect, the more elastic it is the closer it comes to producing pure harmonics. What makes a string more elastic? More length. Pianos which have very short strings have a poor inharmonicity profile because the strings cannot vibrate as freely. That is what gives spinet pianos their nasal tone. On spinet pianos, the last note must be tuned a whopping 50 cents sharp to account for inharmonicity! Pianos which have very long strings have a good inharmonicity profile, and thus produce much purer octaves. A 9 foot concert grand is going to sound much more in tune than a 4’8″ baby grand. If you are thinking of purchasing a grand piano try to get one that is at least 5’6″.
Although this discussion may sound similar to something called Equal Temperament, it is not. Equal temperament defines the ideal tuning for 12 notes in the center of the piano. It makes not stipulations about how octaves should be tuned, and assumes that all octaves are tuned at a 2:1 ratio. Inharmonicity on the other hand deals specifically with octaves and specifies how much “octave stretch” should be used for a given instrument. In the days before electronic tuning devices, tuners simply listened to how the octaves sounded and guesstimate accordingly. Now with the benefits of modern technology we can calculate the amount of octave stretch exactly.
You might be thinking that the effect of inharmonicity is probably so small that only an expert can hear it. Think again. If inharmonicity is not taken into account, the piano will sound so awful that even a non-musician can easily hear the difference. Calculating the inharmonicity is the first and most critical step that we perform to achieving an excellent tuning result.